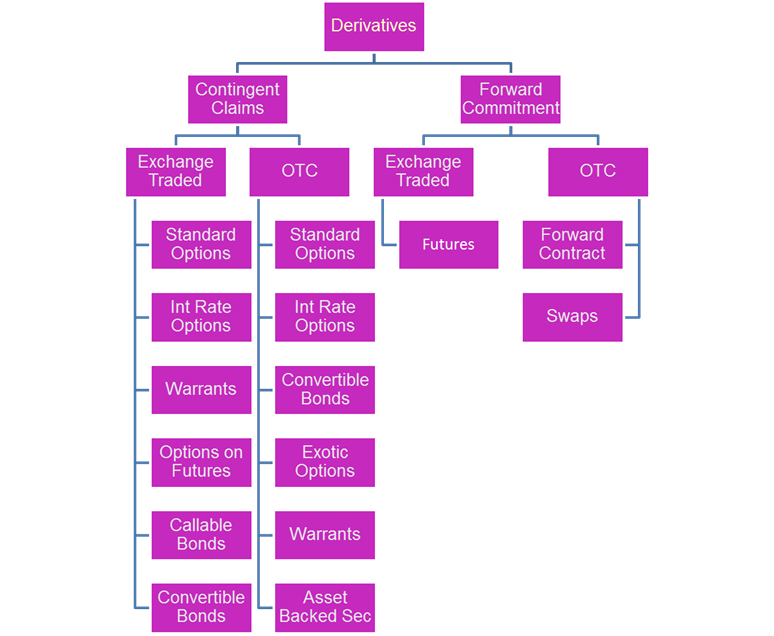
There are two main types of derivatives risk profiles:
- linear derivatives (Forward Commitments)
- non-linear derivatives (Contingent Claims)
A linear derivative is one whose payoff function is symetrical (= linear function). For example, a futures contract has a linear payoff in that every one-tick movement translates directly into a specific cash value per contract (the gain of one side is the symetrical loss of the other side). A Future & Forward commitment is an agreement between two parties in which one party agrees to buy and the other agrees to sell an asset at a future date at a price agreed on today. In essence, a forward commitment represents a commitment to buy or sell. Based on the symetrical rights and obligations of the parties that enter into the contract the payoff function is symetrical (see graphical representation of Forwards below).
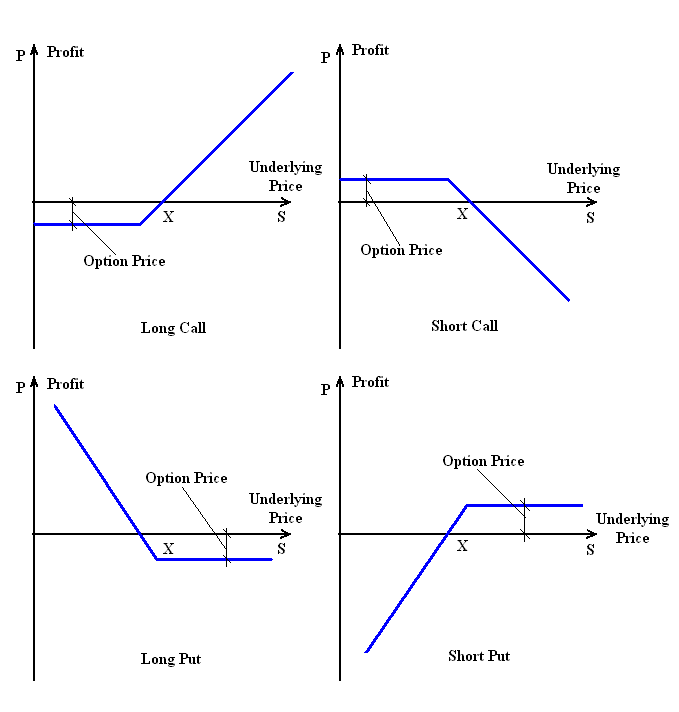
A non-linear derivative is one whose payoff changes with time and space. Space in this case is the location of the strike with respect to the actual price rate (or spot rate). One example of a non-linear derivative with a convex payoff profile at some point before the option's maturity is a simple "plain vanilla" option. A contingent claim is a derivative contract with a payoff dependent on the occurrence of a future event. It can be either Exchange-Traded or OTC. Based on the asymetrical rights and obligations of the parties that enter into the contract, the payoff profile is convex (one party has the right and the other has the obligation). See graphical representation of Options below:
* Notional Amounts
Another aspect of financial derivatives is the fact that they are carried off-balance sheet, generally. When we speak of the size of a particular derivative contract, we refer to the notional amount.
The notional amount is the amount used to calculate the payoff. Because the payoffs of derivative products differ from the payoffs that their notional amounts might suggest if they were cash instruments, they are kept off balance sheet. Otherwise, the balance sheet could be distorted and inflated by even a relatively small derivatives portfolio.
* Volatility
Volatility is the measure of how much the spot rate (price rate of the underlying) is expected to move around. Obviously, in a high volatility environment, the spot rate will be expected to move around aggressively and options premiums are very high. In a low volatility environment, the spot rate is expected to move around very little and options premiums are very low. One of the key factors in making money in options is to understand the nature of volatility. There are two important characteristics of volatility one needs to understand:
- First, volatility is not constant. It changes over the course of time. There might be specific events that will cause volatility to spike higher. For example, the 1992 European Exchange Rate Crisis, triggered by votes on the Maastricht Treaty, turned a relatively stable environment into a savagely volatile one.
- Second, volatility is statistically persistent. That is a fancy way of saying that volatility trends. If it's volatile today, then it should continue to be volatile. If it's calm today, then it should continue to be calm.
Hedging, Speculating and Arbitrage in derivatives (specially with options) often means realizing that the trend in volatility has changed from calm to volatile or vice versa.